Three methods for dissolving a powder in water show a different time (in minutes) it takes until the powder dissolves fully. The results are summarised in Figure 1.
There is an assumption that the population means of the three methods Method 1, Method 2 and Method 3 are not all equal (i.e., at least one method is different from the others). How can we test this?
One way is to use multiple two-sample t-tests and compare Method 1 with Method 2, Method 1 with Method 3 and Method 2 with Method 3 (comparing all the pairs). But if each test is 0.05, the probability of making a Type 1 error when running three tests would increase.
Figure 1: Data for Dissolving a Powder (in Minutes)
A better method is ANOVA (analysis of variances), which is a statistical technique for determining the existence of differences among several population means. The technique requires the analysis of different forms of variances – hence the name. But note: ANOVA is not a test to show that variances are different (that is a different test); it is testing whether means are different.
To perform this ANOVA, the following steps must be taken:
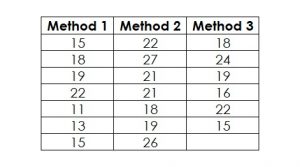
1. Plot the Data
For any statistical application, it is essential to combine it with a graphical representation of the data. Several tools are available for this purpose. They include the popular stratified histogram, dotplot or boxplot.
The boxplot in Figure 2 shows that the dissolution time for Method 1 seems lowest and for Method 2 seems highest. However, there is a certain degree of overlap between the data sets. Therefore, based on this plot, it is risky to draw a conclusion that there is a significant (i.e. statistically proven) difference between any of these methods. A statistical test can help to calculate the risk for this decision.
Figure 2: Boxplot of Data for Different Methods
2. Formulate the Hypothesis for ANOVA
In this case, the parameter of interest is an average, i.e. the null-hypothesis is
H0: μ1 = μ2 = μ3,
with all μ being the population means of the three methods to dissolve the powder.
This means, the alternative hypothesis is
HA: At least one μ is different to at least one other μ.
3. Decide on the Acceptable Risk
Since there is no reason for changing the commonly used acceptable risk of 5%, i.e. 0.05, we use this risk as our threshold for making our decision.
4. Select the Right Tool
If there is a need for comparing more than two means, the popular test for this situation is the ANOVA.
5. Test the Assumptions
Finally, the prerequisites for the ANOVA, the analysis of variances, to work properly are:
- All data sets must be normal and
- All variances must not be significantly different from each other.
Figure 3: Descriptive Statistics for Dissolving a Powder (in Minutes)
Firstly, since all samples show a p-value above 0.05 (or 5 percent) for the Anderson-Darling Normality test (Figure 3), we can conclude that all samples are normally distributed. The test for normality uses the Anderson Darling test for which the null hypothesis is “Data are normally distributed” and the alternative hypothesis is “Data are not normally distributed.”
Secondly, as an alternative to perform a test for equal variances, it is appropriate to check whether the confidence intervals for sigma (95% CI Sigma) overlap. If there is a large overlap, the assumption for no significant difference between the variances is valid.
This means, both prerequisites for ANOVA are met.
Figure 4: ANOVA Test Statistics
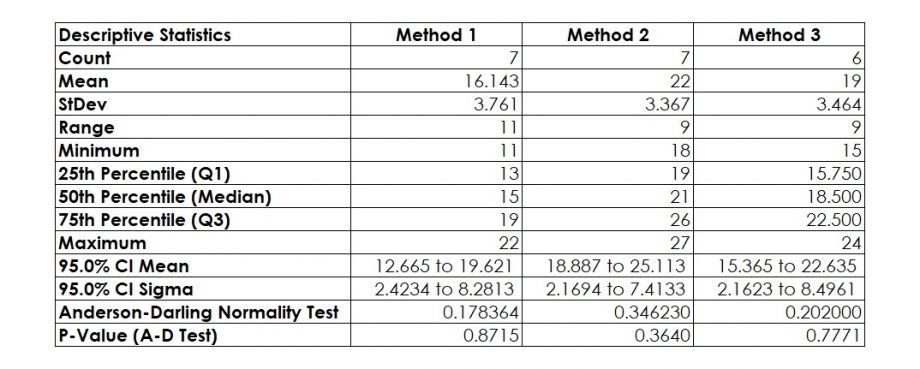
6. Conduct the Test
Using the ANOVA, the analysis of variances, statistics software SigmaXL generates the output in Figure 4.
Since the p-value is 0.0223, i.e. less than 0.05 (or 5 percent), we reject H0 and accept HA.
7. Make a Decision
With this, ANOVA statistics means that there is at least one significant difference.
Additionally, this statistics shows which method is different from which other method. The p-value for pairwise comparison is 0.0066 between Method 1 and Method 2, i.e. there is a significant difference between Method 1 and Method 2. The boxplot shows the direction of this difference.
Finally, the statistics informs that this X (Methods) covers only 36% of the total variation in the methods. There might be other Xs explaining part of the rest variation of 64%.
Interested in the stats? Read here.
